TEOREMA VALOR MEDIO
En cálculo diferencial, el teorema de
valor medio (de Lagrange), teorema de los incrementos finitos, teorema
de Bonnet-Lagrange o teoría del punto medio es una
propiedad de las funciones derivables en un intervalo. Algunos matemáticos consideran que este teorema es el más importante del cálculo (ver
también el teorema fundamental del cálculo integral). El teorema no se usa para resolver problemas matemáticos;
más bien, se usa normalmente para demostrar otros teoremas. El teorema de valor medio puede usarse
para demostrar el teorema de Taylor, ya que
es un caso especial.
HISTORIA
Un caso especial de este teorema fue descrito por primera vez
por Paramésuara (1370–1460),
de la escuela de Kerala de astronomía y matemáticas en la India, en sus comentarios sobre Govindasvāmi y Bhaskara II.1 Una forma restringida del teorema fue demostrada por Michel Rolle en 1691; el resultado fue lo que ahora se
conoce como teorema de Rolle, y se
demostró sólo para polinomios, sin las técnicas de cálculo. El teorema del
valor medio en su forma moderna fue declarado y probado por Cauchy en 1823.
ENUNCIADO PARA UNA VARIABLE
En esencia, el teorema dice que dada cualquier función f continua
en el intervalo [a, b] y derivable en el intervalo abierto (a, b),
entonces existe al menos algún punto c en el intervalo (a, b)
tal que la tangente a la curva en c es paralela a la recta
secante que une los puntos (b, f(b)) y (a, f(a)).
Es decir:
Este teorema lo
formuló Lagrange.
El teorema del valor medio de Lagrange, de hecho, es una
generalización del teorema de Rolle, que dice que si una función es
definida y continua [a, b], diferenciable en el intervalo
abierto (a, b), y toma valores iguales en los extremos del
intervalo – en otras palabras, f(a) = f(b)
– entonces existe al menos algún punto c en el intervalo (a, b)
tal que la tangente a la curva en c es horizontal, es
decir f'(c) = 0.

Para una función que cumpla la hipótesis de ser definida y continua [a, b] y derivable en el intervalo abierto (a, b) entonces existe al menos algún punto cen el intervalo (a, b) en que la pendiente de la curva es igual que la pendiente media de la curva en el intervalo cerrado [a, b].
Teorema del valor medio o de Lagrange
En esta lección te voy a explicar qué dice y cómo se interpreta el
teorema del valor medio, también conocido como teorema de Lagrange o de los
incrementos finitos. Este teorema se explica en 2º de bachillerato cuando se
estudian las aplicaciones de las deviradas.
El teorema del valor medio dice así:
Si tenemos una función f(x) continua en el intervalo cerrado [a,b]
(tiene que ser continua en x=a y x=b) y derivable en el intervalo abierto
(a,b) (no tiene por qué ser derivable ni en x=a ni en x=b), entonces, existe al
menos un punto c, perteneciente al intervalo abierto (a,b), tal que en ese
punto se verifica:

Además, f(a) y f(b) tienen que ser distintas.
Simbólicamente, lo podemos expresar así:

¿Y esto que significa?
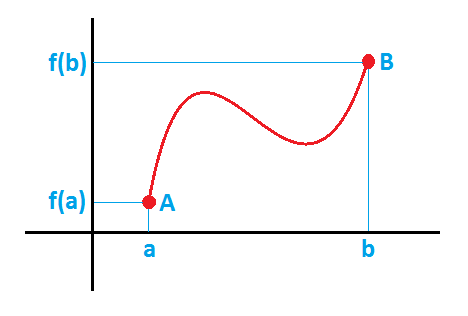
Tenemos una función f(x) que es continua en [a,b], derivable en (a,b),
como esta:
Los puntos x=a y x=b, pertenecen a la función y vemos también que
el punto x=a, tiene un valor de la función f(a) y el punto b tiene un
valor de la función f(b) que es distinto de f(a).
Por tanto, esta función cumple las condiciones para que se cumpla el teorema
del valor medio.
Si trazamos una recta que pase por los puntos A y B:

La pendiente de esa recta, tiene la siguiente fórmula:

Que corresponde a la pendiente de una recta que pasa por dos puntos.
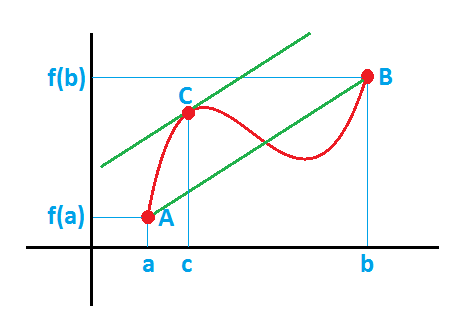
Lo que dice el teorema del valor
medio es que si se cumplen todas las condiciones anteriores, que hemos visto
que sí, entonces existe al menos un punto c, en el cual, la recta tangente
en ese punto, es paralela a la recta que pasa por
los puntos A y B:

La ecuación de la pendiente de la recta tangente en un punto es igual a
la derivada de la función en ese punto. Por tanto, en el punto c, la ecuación
de la pendiente de la recta tangente será:

Cuando dos rectas son paralelas, significa que tienen la misma
pendiente, por lo que la pendiente de la recta tangente en el punto c y la
pendiente de la recta que pasa por A y B son iguales y por tanto:

El teorema del valor medio dice que existe al menos un punto c, que
verifica todo lo anterior, o en otras palabras, que puede existir más de un
punto
En este caso, como vemos en la gráfica de la función, tenemos otro punto
d donde la recta tangente a la función es paralela a la recta que pasa por A y
B:
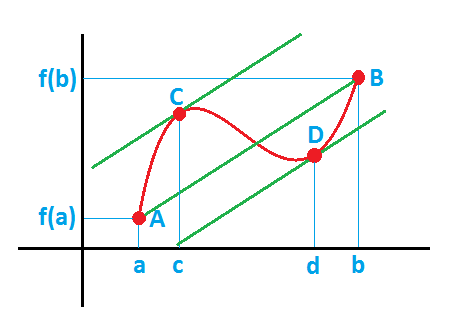
Por tanto, en ese punto también se cumple:

Cómo
aplicar el teorema del valor medio. Ejercicios resueltos
Vamos a ver ahora algunos ejemplos de
cómo aplicar el teorema del valor medio y calcular el punto c del teorema.
Ejemplo
1
Calcula el punto c
que satisface el teorema del valor medio para la siguiente función en el
intervalo [0,1]:

En primer lugar, debemos comprobar si
se cumplen las condiciones para que se pueda aplicar el teorema del valor
medio. Debemos comprobar si la ecuación es continua en [0,1] y derivable en
(0,1)
Continuidad:
La función es continua en todo R, al
ser una función polinómica, por lo que también será continua en el intervalo
[0,1].
Derivabilidad:
La función es derivable en (0,1) si
su derivada es continua en ese intervalo.
La derivada de la función es:

Que es continua en todo R al ser una
función polinómica, por tanto f(x) es derivable.
Es continua en [0,1] y derivable en
(0,1), por tanto, existe un valor de c en ese intervalo tal que:

Vamos a pasar a calcular el punto c
del teorema.
Calculamos lo que vale la función en
los extremos del intervalo:


Y calculamos f'(c):

Por otro lado, calculamos f'(c) a
partir de f'(x):

Sustituyendo la x por la c:

Igualamos ambos resultados de
f'(c) y nos queda una ecuación que depende de c y de donde podemos despejarla y
encontrar el valor de c que nos están pidiendo:

VIDEOS TUTORIALES:
https://www.youtube.com/watch?v=q6jhJEX9lug
https://www.youtube.com/watch?v=1_Vp4YX7twU
https://www.youtube.com/watch?v=gjhlwU39Sro
No hay comentarios.:
Publicar un comentario